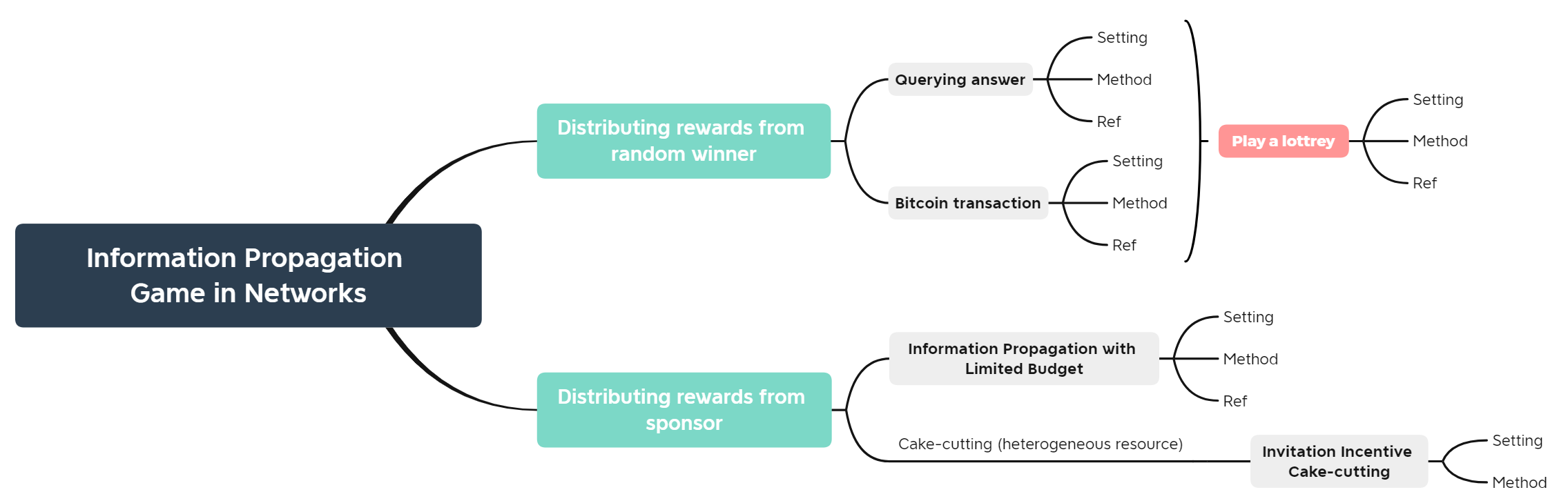
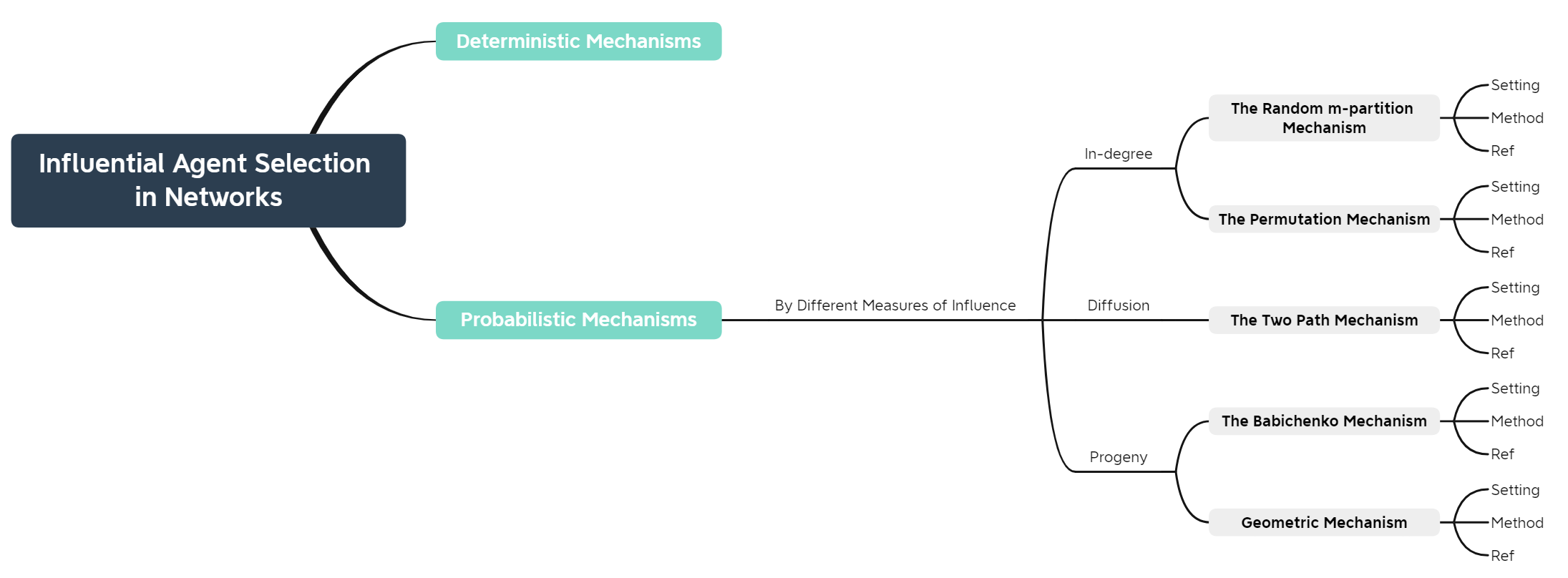
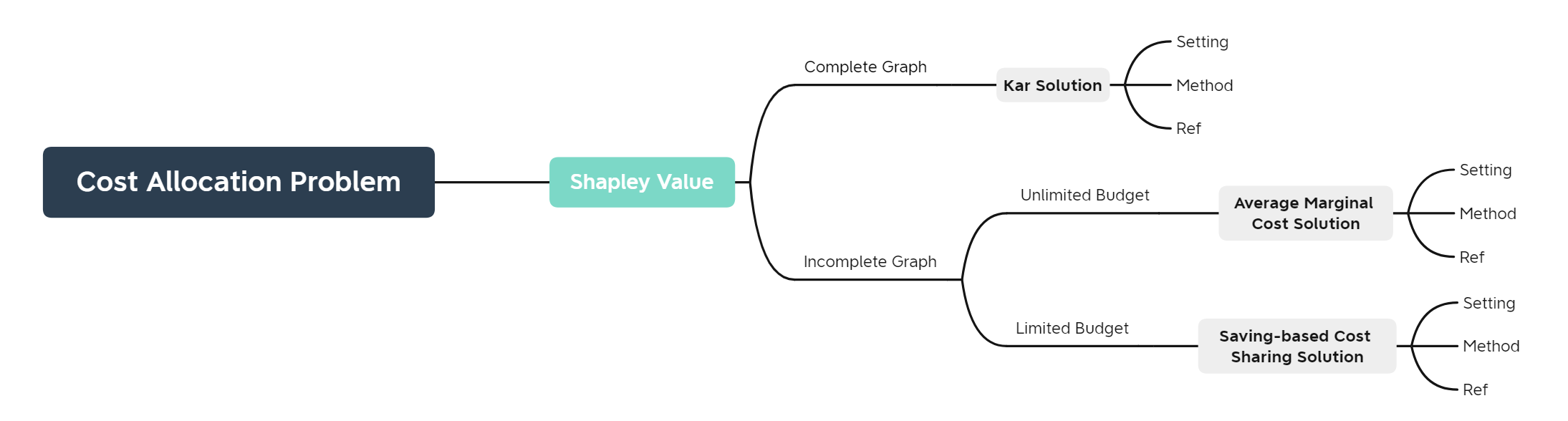
Querying answer[1]
Setting
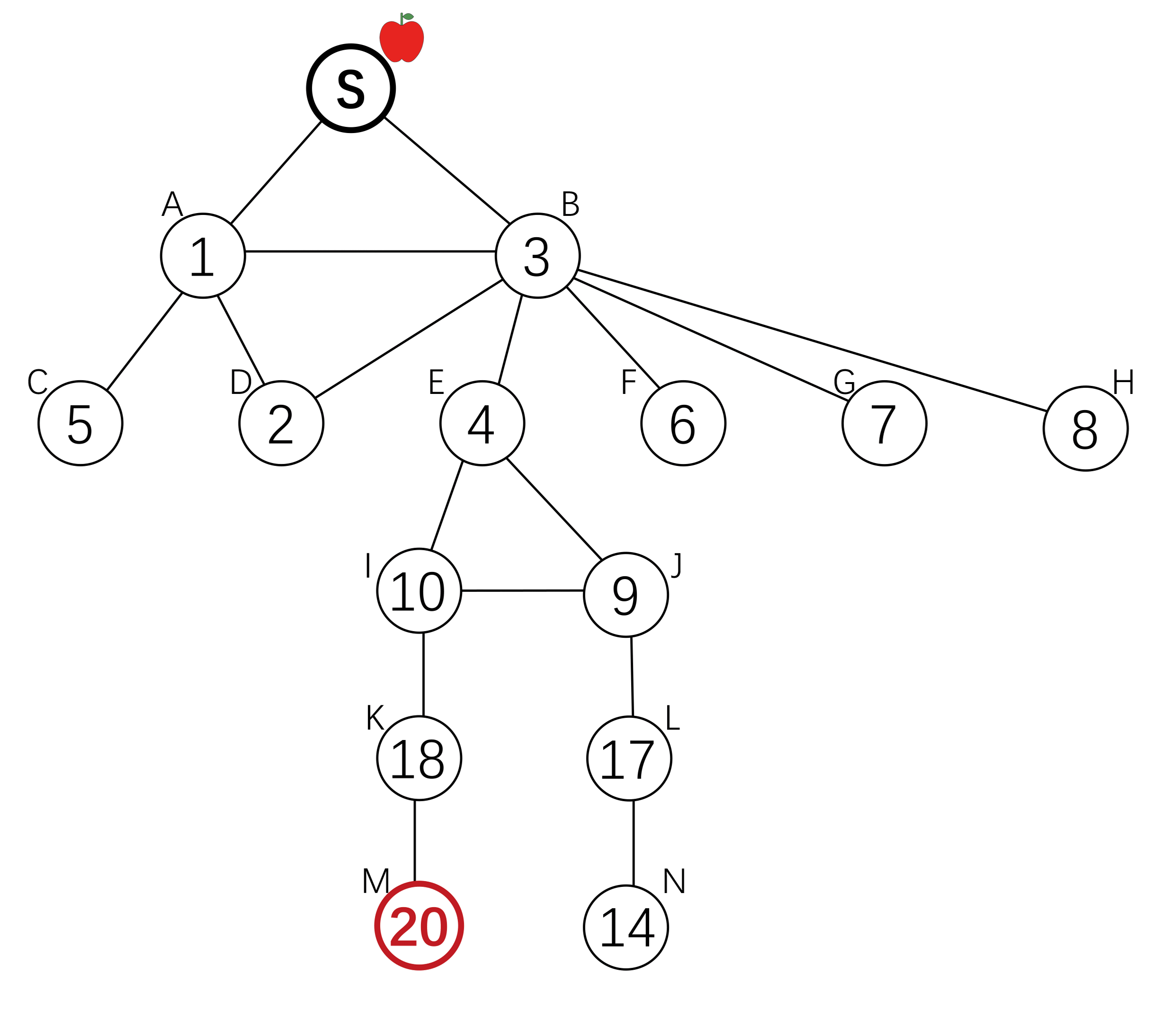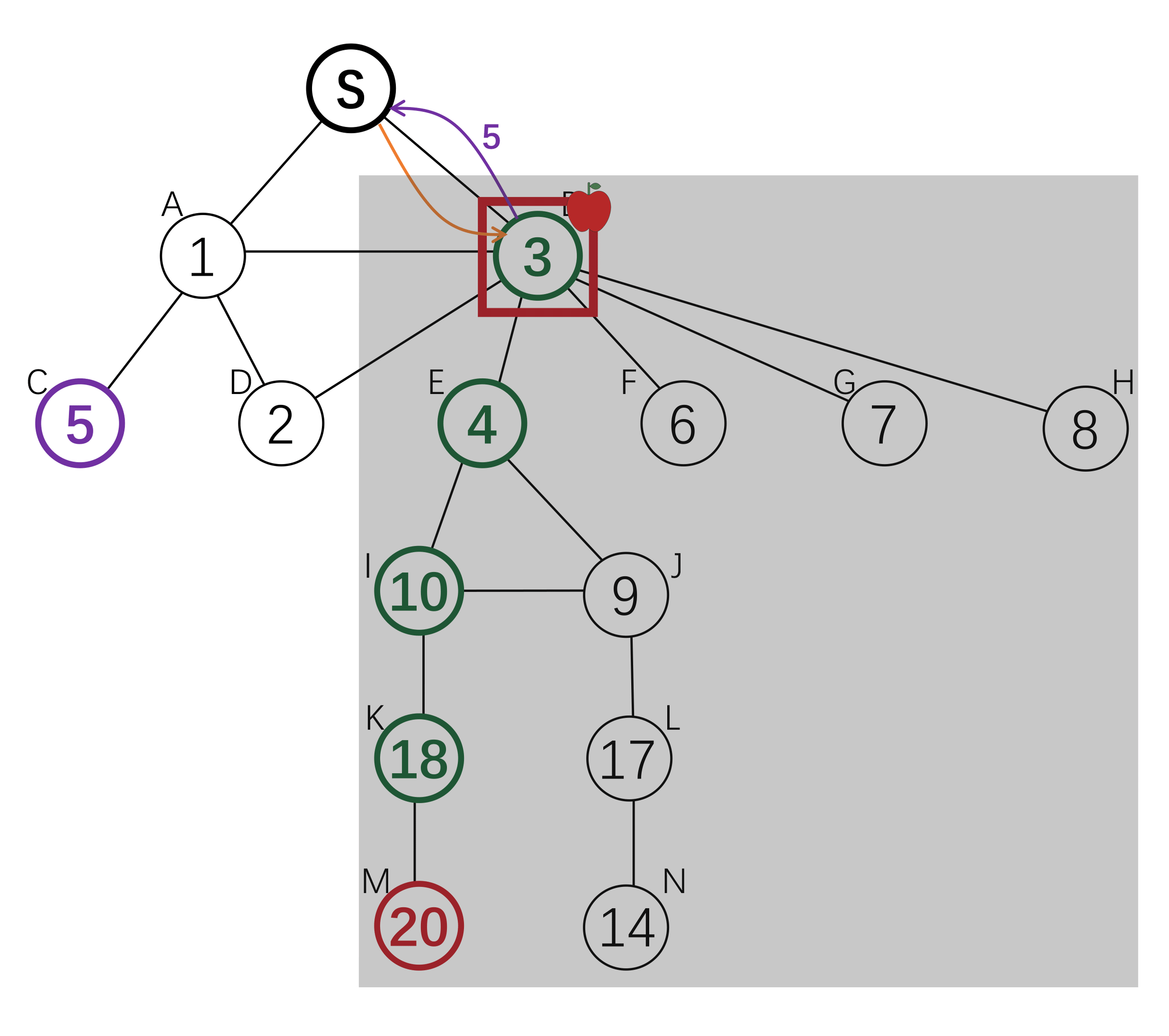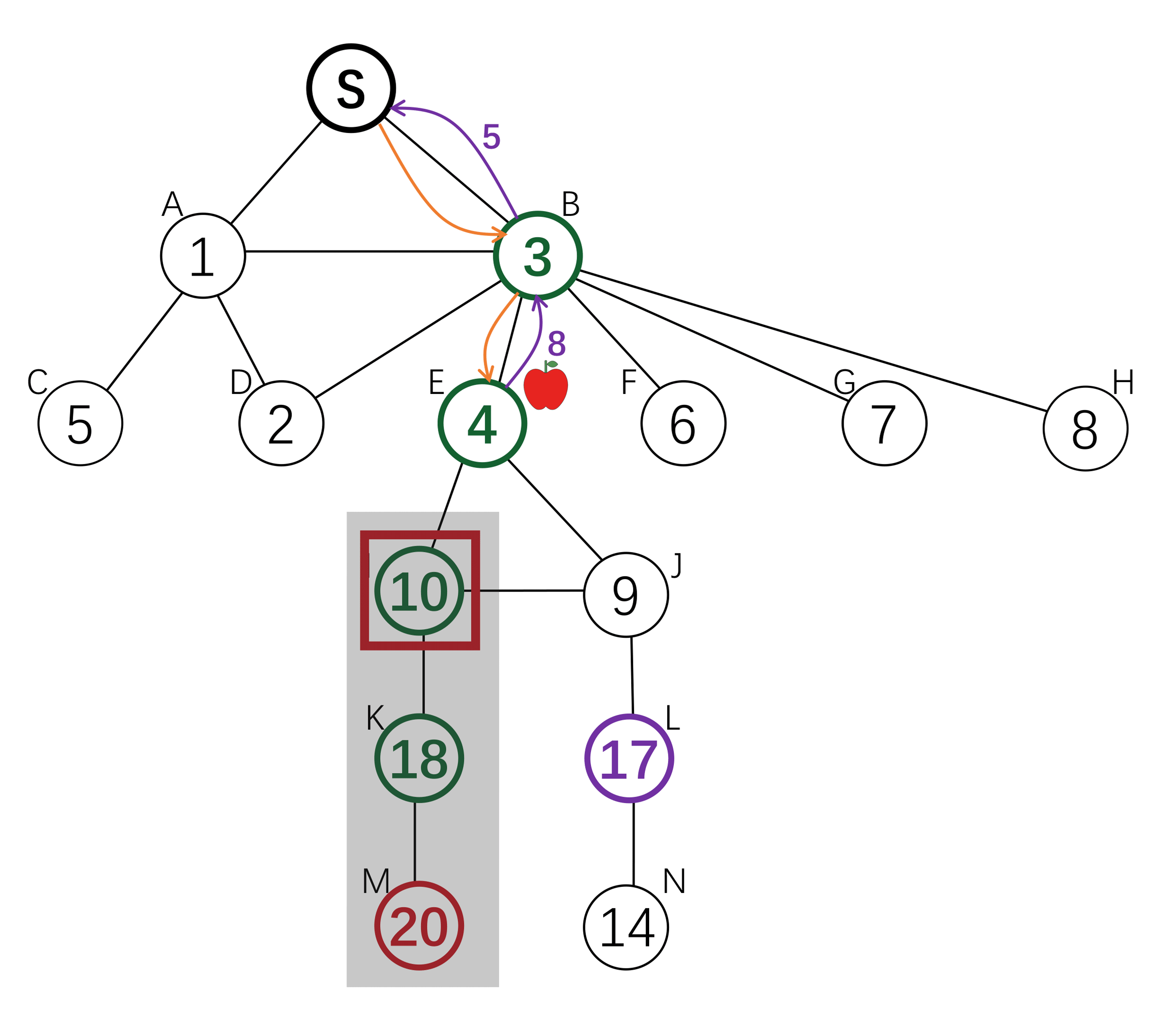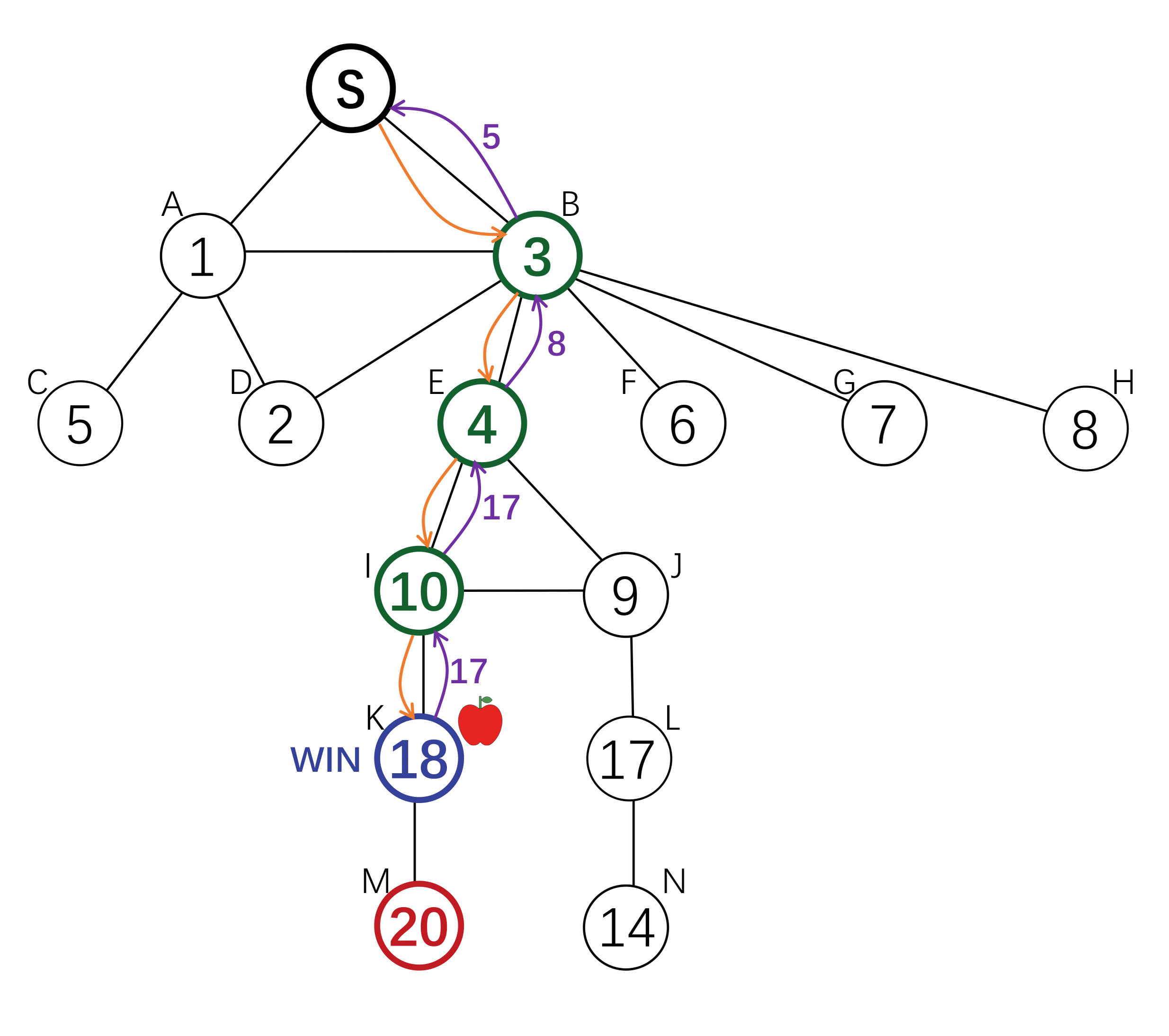
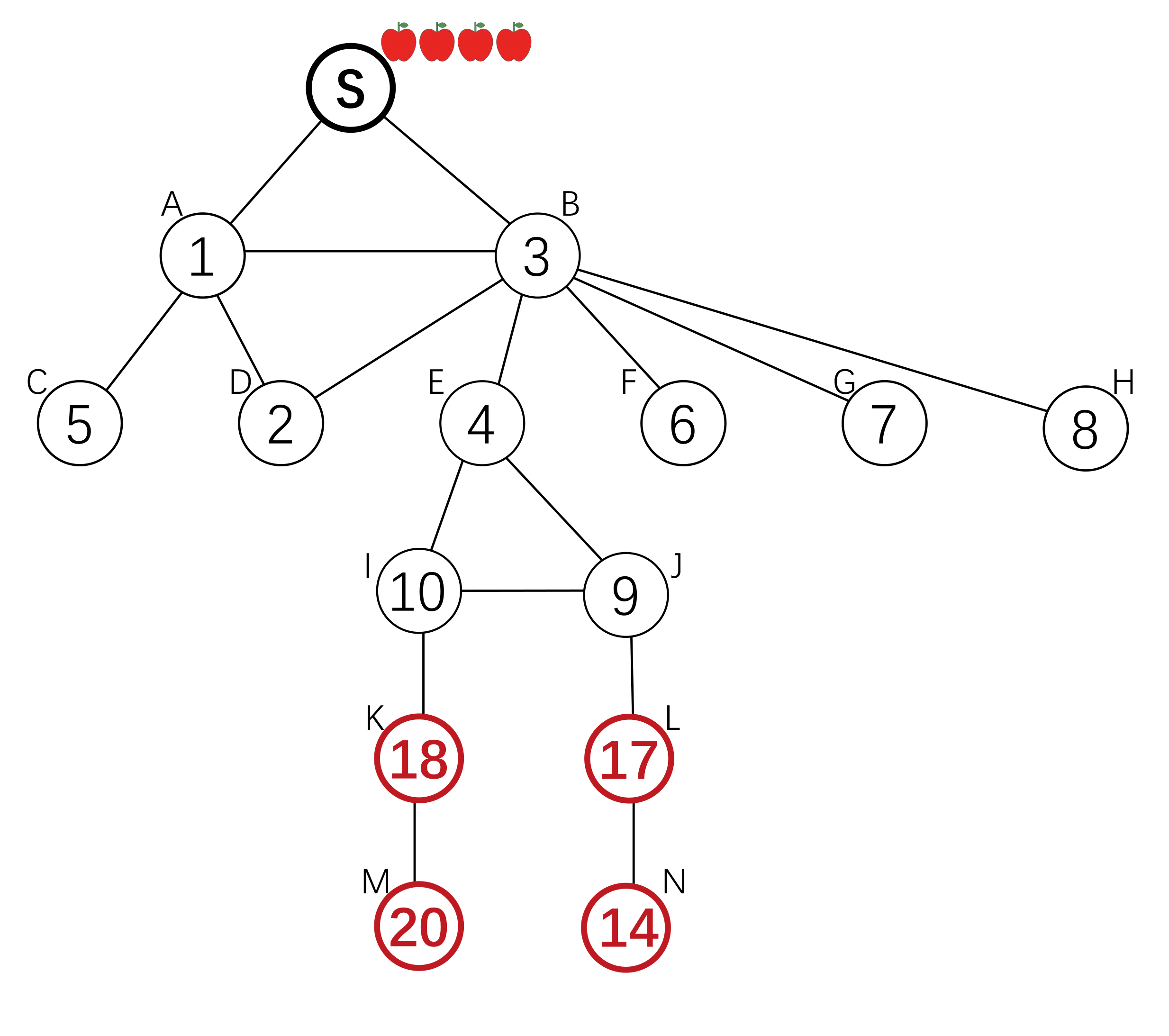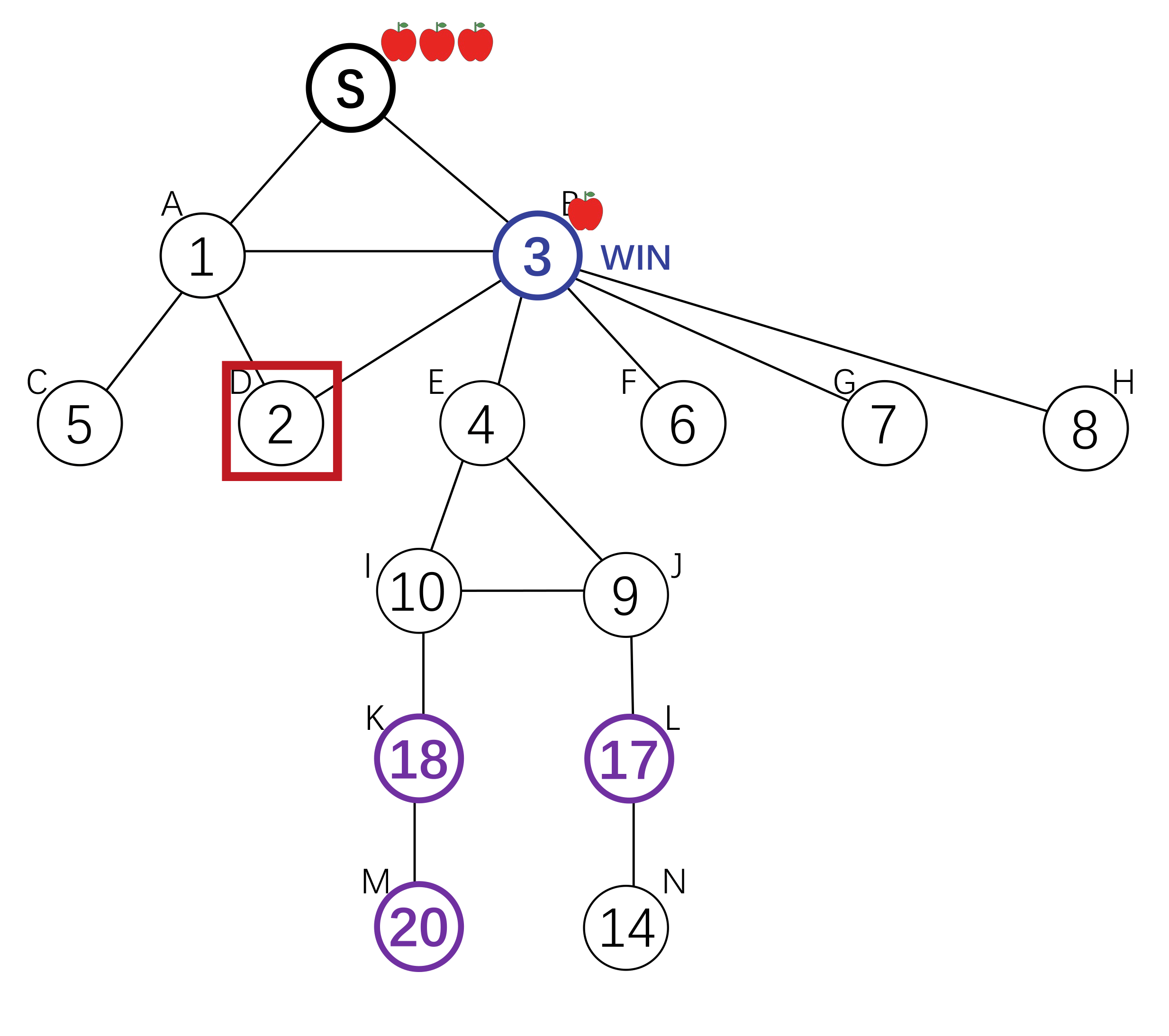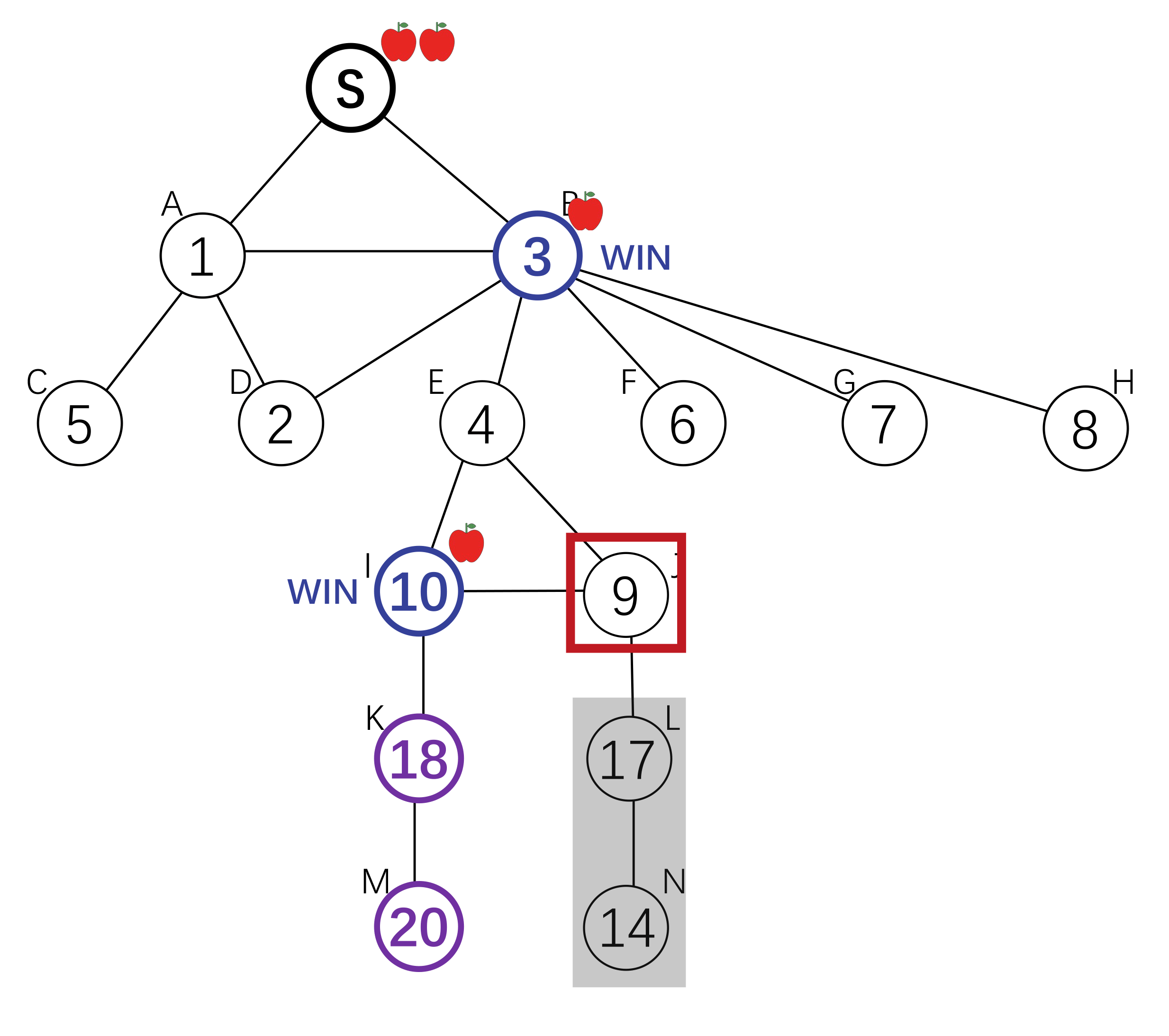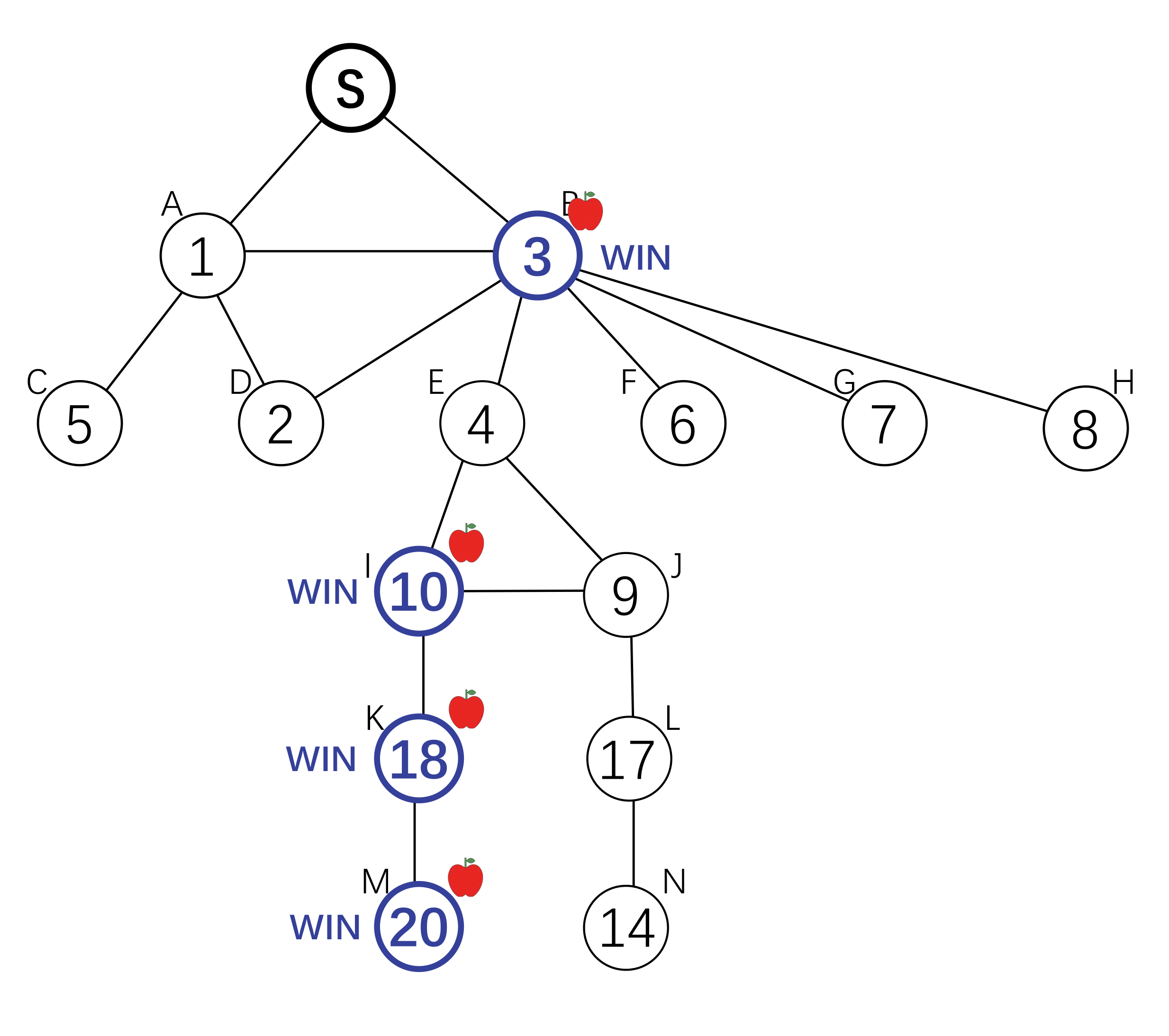
The root node wants to find an answer to some questions. She incentivizes her neighbours to find the answer holder among their children. The parents of the answer holder will get a reward.
Method
To incentivize invitation, each node is offered a reward by its parent, and offers a (smaller) reward to its children. The search down each branch stops when the reward reaches 0, or when a node with an answer is reached. There exists a Nash Equilibrium where each node will invite all her neighbours, and the reward amount is defined by a computable function g(x). Each agent will offer g(x) to its children on receiving x, where g(x) is the amount that maximize her expected utility.
Bitcoin transaction[2]
Setting
There is a bitcoin transaction, and miners can try to "authorize" a transaction. The root node uses a reward distribution scheme to invite more miners aware of this transaction. Once there is a node success to authorize it, agents in the chain from seed to node are all rewarded.
Method
(β,H)-almost-uniform scheme was used to incentivize miners to broadcast the transaction. In this scheme, we should find the chain from seed to the winner, with length l. If l ≤H, then the winner is rewarded 1+(H-l+1)β, other nodes in the chain get β. If l>H, no nodes get rewards. Under this scheme, each node’s dominant strategy is full propagation and no duplicate.
Playing lotteries[3]
Setting
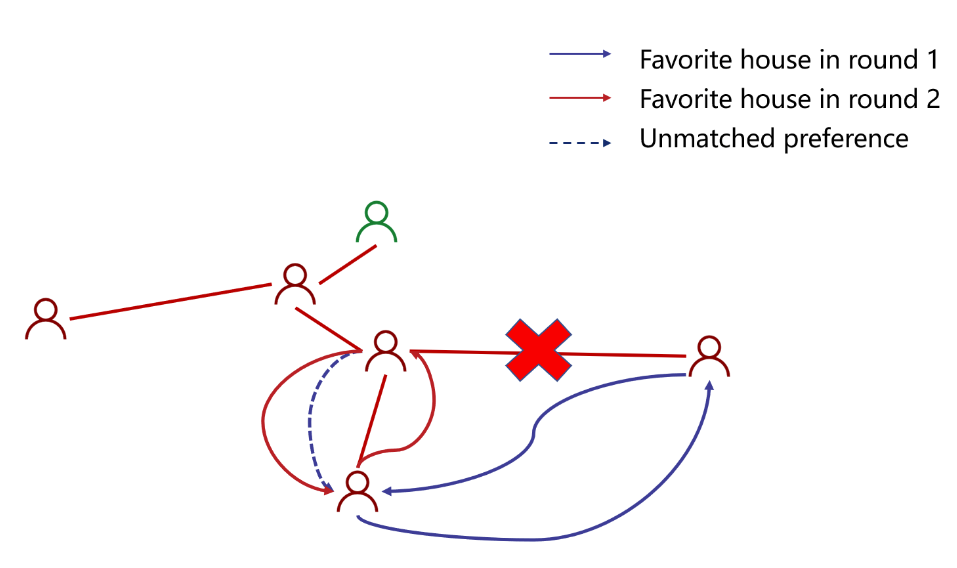
The sender provides a monetary reward by a lottery, which all participants have equal chance to win. Initially, only the sender's friends are in the game.
However, the sender wants to invite as more participants as possible to join the game.
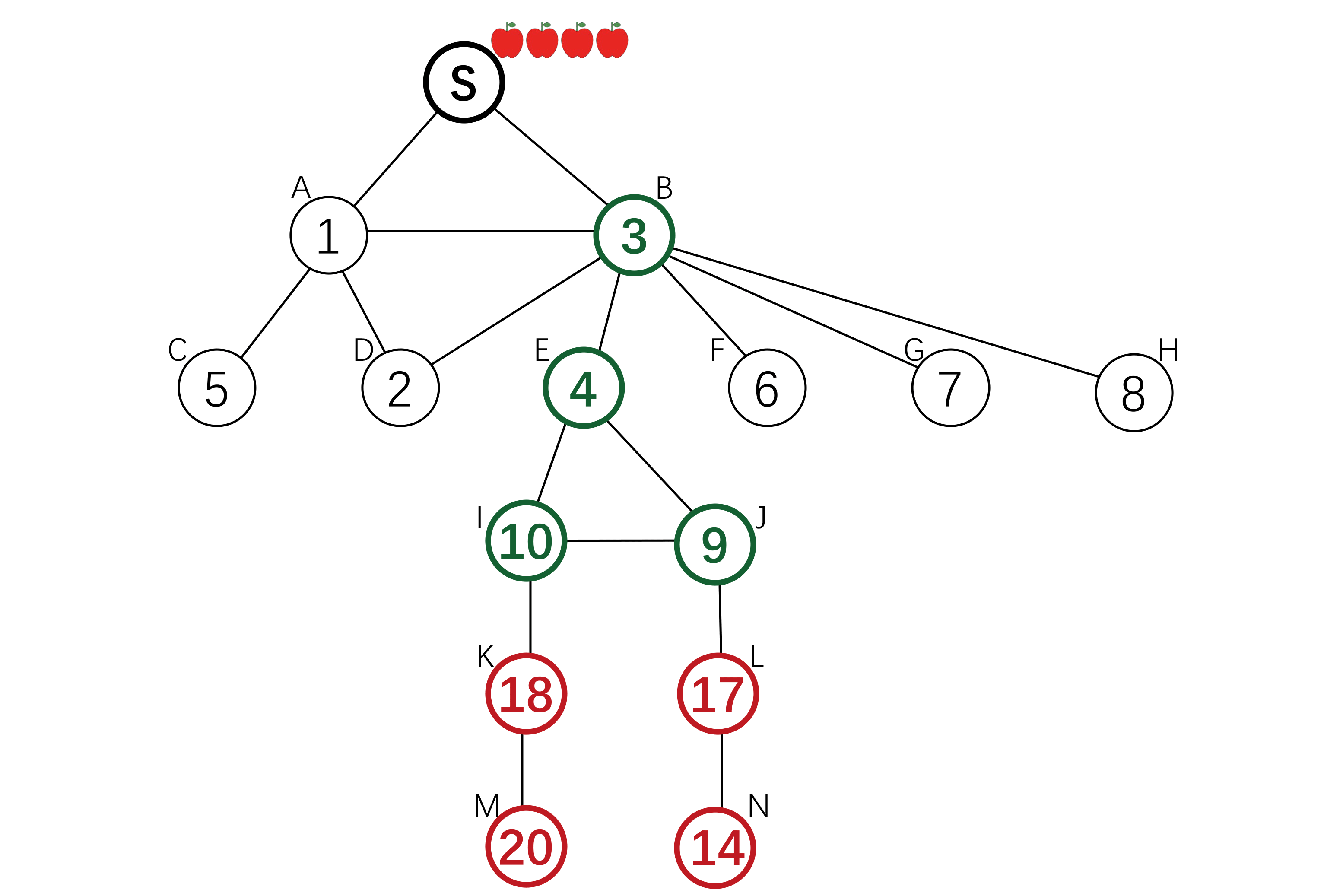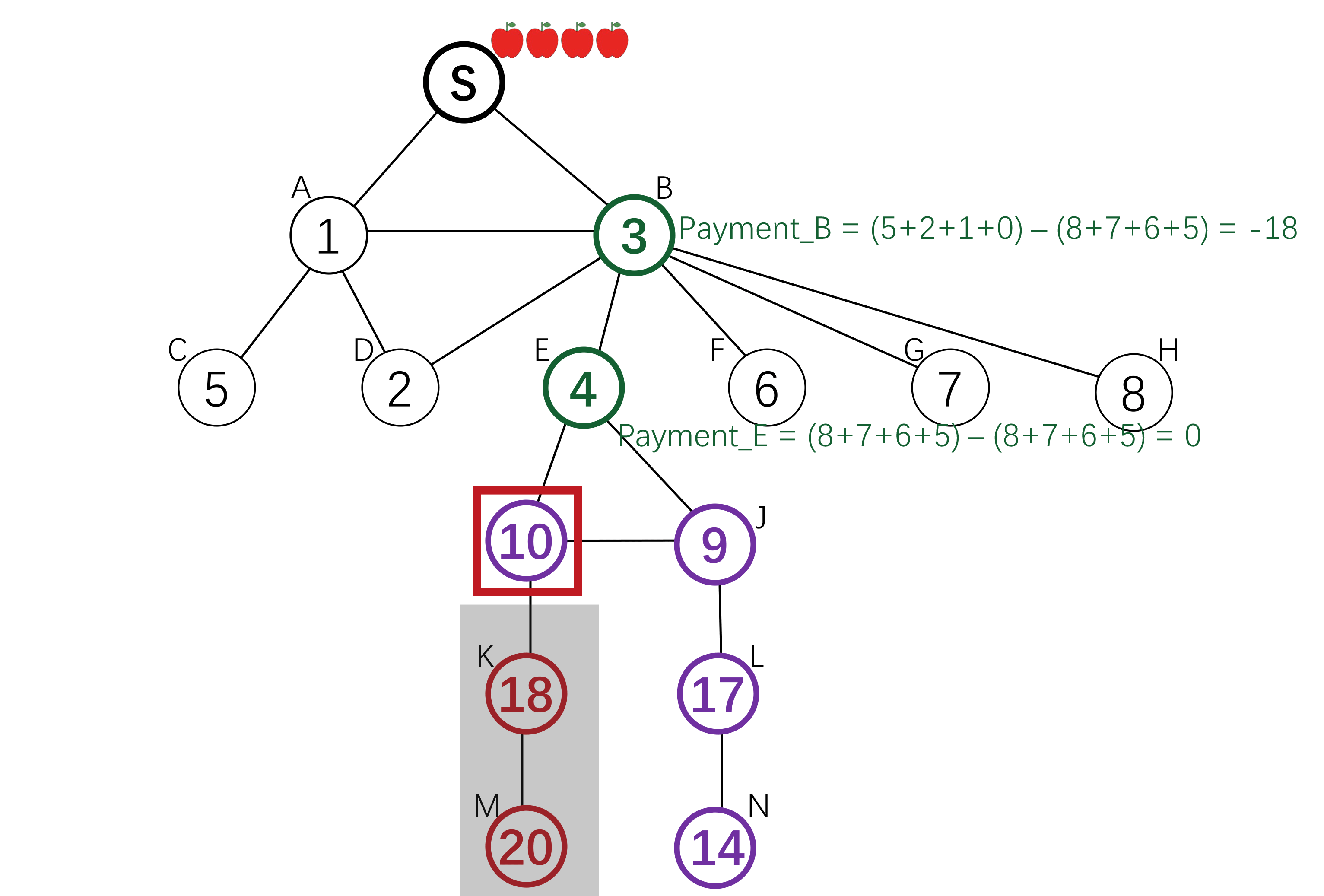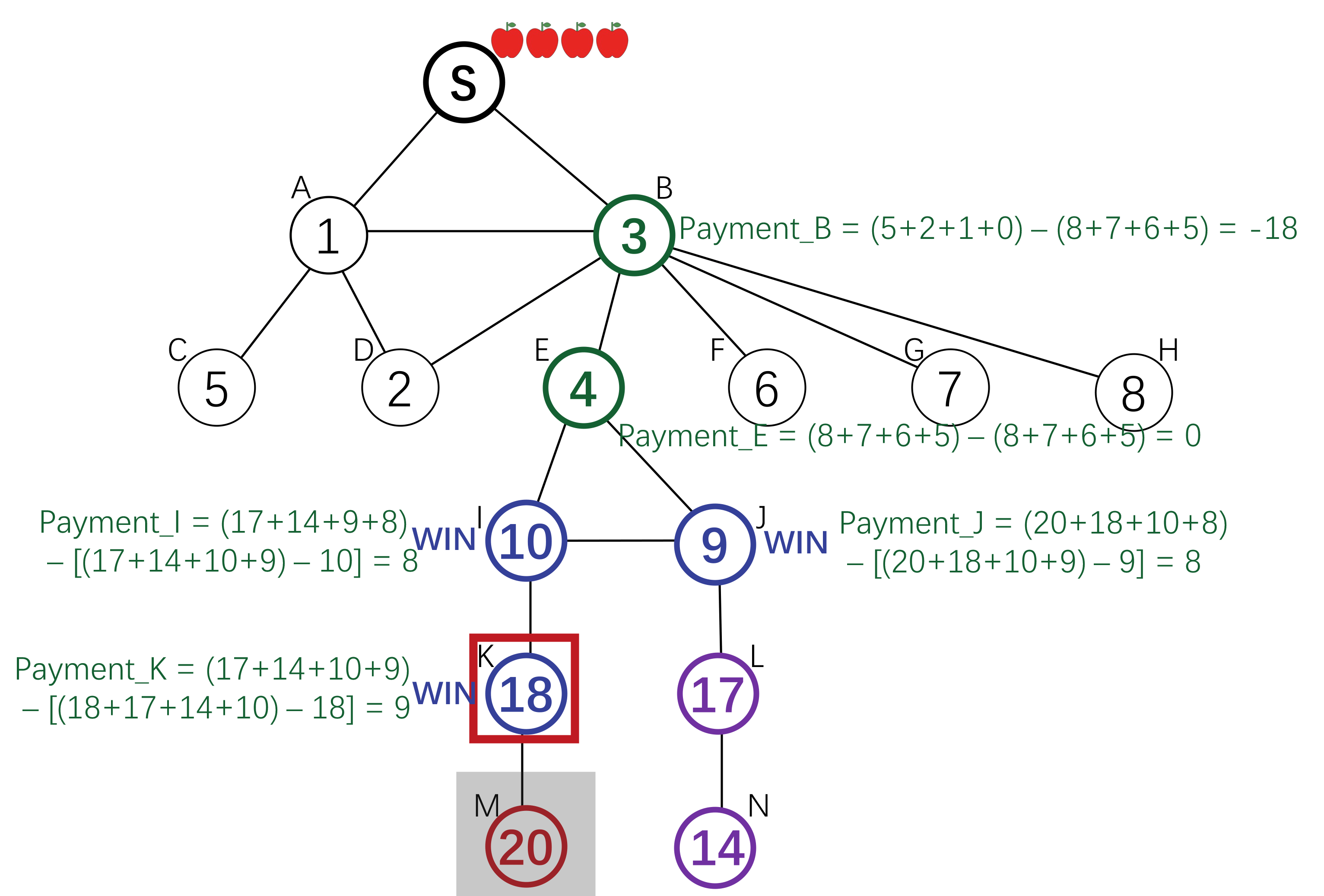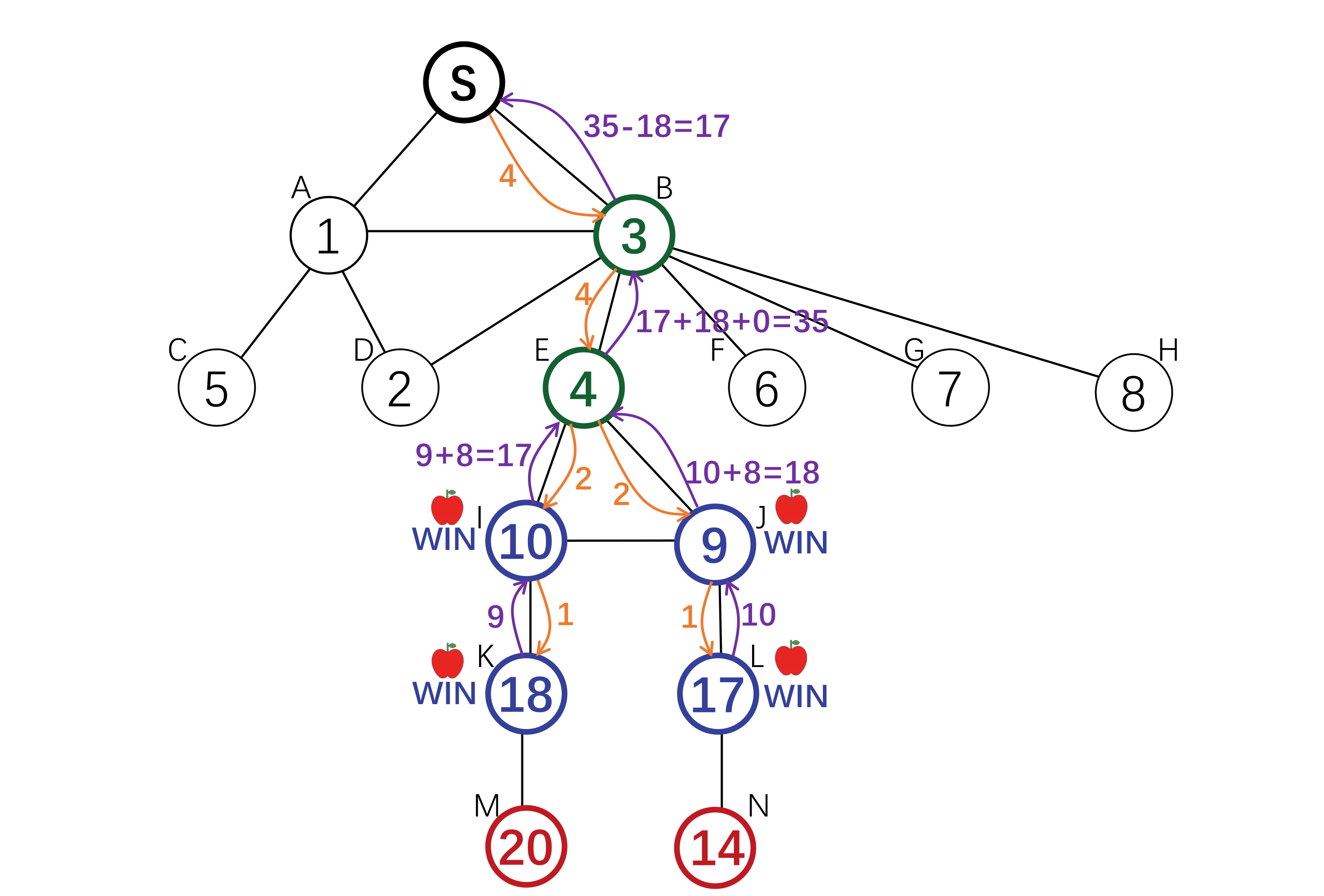
Method
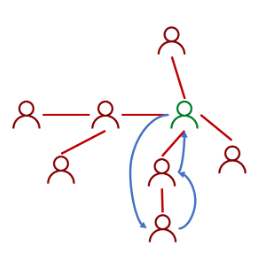
Initially, each node only has a small probability to win. She can increase her utility by inviting her friends to join. If one of the friends wins, she withholds part of the reward and gives the remaining part to the winner. In this way, she can increase her winning chance by expanding her subtree. Other nodes will adopt the same strategy to increase the expected utility. This work designs a free market, where each participant can invite any of her neighbours and decide by herself the amount of reward to withhold. There is a Nash Equilibrium where each agent invites all friends and withholds a sufficiently small amount of rewards.
Information Propagation with Limited Budget[4]
Setting
The sponsor has a monetary budget and is willing to propagate some information via social networks. The goal is to design a budget distribution scheme where all of the budgets is distributed, and each agent has an incentive to invite all neighbours.
Method
The agents are divided into layers according to their distance from the sponsor in the graph. Then use peer pressure to inspire competition among agents, hence incentivising them to do further propagation. When an agent propagates, she will get a reward from her competitors. Her reward must be given to other agents at the same time. Adopting this method to all layers, the budget distribution mechanism is IC, IR and budget balance.
Invitation Incentive Cake-cutting
Setting
The setting is similar as before, except the reward provided by the sponsor is heterogeneous, each agent may have different value to different parts of the resource.
Method
The agents are also divided into layers. Initially, the resource is randomly allocated to the first layer's agents. For each layer k in the graph, find all edges that start at layer k and end at layer k+1. Then we visit these edges and reallocate the resource of other agents in layer k to edges' end points. This mechanism incentivizes agents not only to invite all neighbours but also to report their true valuation to the resource. A minimum utility is guaranteed for each agent even if she does not invite anyone.
References
[1] Kleinberg, J., & Raghavan, P. (2005, October). Query incentive networks. In 46th Annual IEEE Symposium on Foundations of Computer Science (FOCS'05) (pp. 132-141). IEEE.
[2] Babaioff, M., Dobzinski, S., Oren, S., & Zohar, A. (2012, June). On bitcoin and red balloons. In Proceedings of the 13th ACM conference on electronic commerce (pp. 56-73).
[3] Chen, J., & Li, B. (2021). Maximal Information Propagation via Lotteries. arXiv preprint arXiv:2110.10606.
[4] Shi, H., Zhang, Y., Si, Z., Wang, L., & Zhao, D. (2020). Maximal Information Propagation with Budgets. In ECAI 2020 (pp. 211-218). IOS Press.